AdaBoost
This post is basically based on Explaining AdaBoost.
What is AdaBoost
AdaBoost is an ensemble learning method. It can construct a ”strong” classifier as linear combination
\[F(x) = \sum_{t=1}^T \alpha_t h_t (x)\]of “simple”, “weak” classifiers \(h_t (x)\)
Specifically, the algorithm is as follows:
Given: \((x_1, y_1),...(x_m,y_m)\) where \(x_i \in \mathscr X\), \(y\in\{-1,+1\}\)
Initialize: \(D_1(i)=1/m\) for \(i=1,...,m\).
For \(t=1,...,T\):
- Train weak learner using distribution \(D_t\).
- Get weak hypothesis \(h_t : \mathscr X \to \{-1, +1\}\)
-
Aim: select \(h_t\) with low weighted error:
\[\varepsilon_t = \text{Pr}_{i\sim D_t} [h_t(x_i)\ne y_i]\] - Choose \(\alpha_t = \frac{1}{2} \ln \left( \frac{1-\varepsilon_t}{\varepsilon_t} \right)\)
-
Update, for \(i=1,...,m\):
\[D_{t+1}(i) = \frac{D_t(i)\exp (-\alpha_t y_i h_t (x_i))}{Z_t}\]where \(Z_t\) is a normalization factor (chosen so that \(D_{t+1}\) will be a distribution).
Output the final hypothesis:
\(H(x) = \text{sign} \left( \sum_{t=1}^T \alpha_t h_t (x) \right)\)
—-
Some comments
Learning speed
Robert E. Schapire’s Explaining AdaBoost provides some insight on the the AdaBoost topic. As we know, the “weak learners” in AdaBoost is suppposed to be “slightly better” than random guess. Based on this assumption, called weak learning condition, it can be proven that training error of AdaBoost’s final hypothesis decreases to zero very rapidly; in fact, in just \(O(\log m)\) rounds (ignoring all other parameters of the problem), the final hypothesis will perfectly fit the training set .
Simpler is better?
Usually for a learned classifier to be effective and accurate in its predictions, it should meet three conditions: (1) it should have been trained on “enough” training examples; (2) it should provide a good fit to those training examples (usually meaning that it should have low training error); and (3) it should be “simple.” This last condition, our expectation that simpler rules are better, is often referred to as Occam’s razor.
However, for boosting, something counter-intuitive happens. According to Explaining AdaBoost., boosting is typically resistance to overfitting, although overfitting can happen in boosting. I borrow two figures from Explaining AdaBoost here to show this feature.
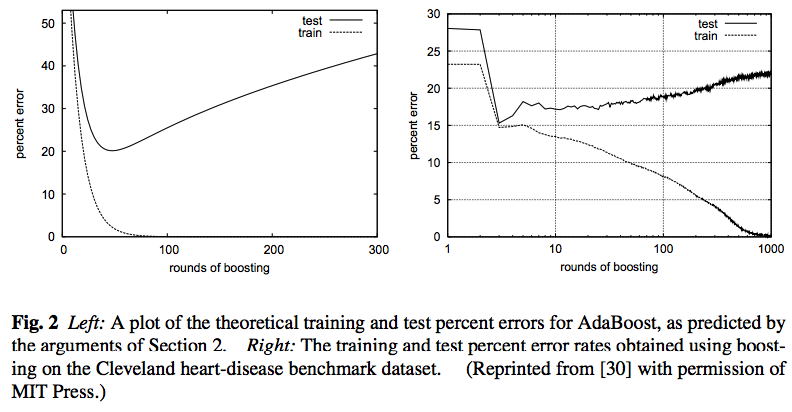
One of the explanation is Margin, a variable to measure the confidence of the model. Margin can be computed as the differences in the voting process in forming \(H\), a vote a conducted among weak learners.
Loss minimization
AdaBoost can be understood as a procedure for greedily minimizing what has come to be called the exponential loss, namely,
\[\frac{1}{m} \sum_{i=1}^m \exp \left( -y_i F(x_i) \right)\]Ref.
The slides, blogs and paper below are referrd in writing this blog.
Boosting and AdaBoost for Machine Learning - Jason Brownlee
AdaBoost - Jiri Matas and Jan Sochman
[1] Freund, Y., & Schapire, R. E. (1995, March). A desicion-theoretic generalization of on-line learning and an application to boosting. In European conference on computational learning theory (pp. 23-37). Springer, Berlin, Heidelberg.
[2] Schapire, R. E. and Freund, Y. (2012). Boosting: Foundations and Algorithms. MIT Press.
