A Summary of Clustering Methods

This post a summary of clustering methods I learned from Data Mining course at UMN.

Basically, clustering methods can be divided into two types: hierarchical and partitional.

Type of Clusters

Well-Separated Clusters

A cluster is a set of points such that any point in a cluster is closer (or more similar) to every other point in the cluster than to any point not in the cluster.

Center-based clusters

A cluster is a set of objects such that an object in a cluster is closer (moresimilar) to the “center” of a cluster, than to the center of any other cluster.

The center of a cluster is often a centroid, the average of all the points in the cluster, or a medoid, the most “representative” point of a cluster.

Contiguity-based clusters

A cluster is a set of points such that a point in a cluster is closer (or more similar) to one or more other points in the cluster than to any point not in the cluster.

Density-based clusters

A cluster is a dense region of points, which is separated by low-density regions, from other regions of high density. Used when the clusters are irregular or intertwined, and when noise and outliers are present.

Clusters Algorithms

More about K-meanas and Hierarchical clustering can be found in another post.

K-means Clustering

Sum of Squared Error (SSE) is usually used to evaluate K-means.

\[SSE=\sum_{i=1}^K\sum_{x\in C_i}\text{dist}^2(m_i,x)\]

K-means has problems when clusters are of differing sizes, densities and non-globular shapes.

K-means has problems when the data contains outliers.

Choosing initial centroids is very important for K-means.

Hierarchical Clustering

Strengths of Hierarchical Clustering:

• Do not have to assume any particular number of clusters.
• They may correspond to meaningful taxonomies.

Key operation is the computation of the proximity of two clusters.

We have the following ways to define the inter-cluster distances: MIN, MAX, Group Average, Distance Between Centroids

MIN: Single link, can handle non-elliptical shapes.

However, single link is sensitive to noise and outliers

MAX: Complete link, less susceptible to noise and outliers.

The limitations of MAX is:

• Tends to break large clusters
• Biased towards globular clusters

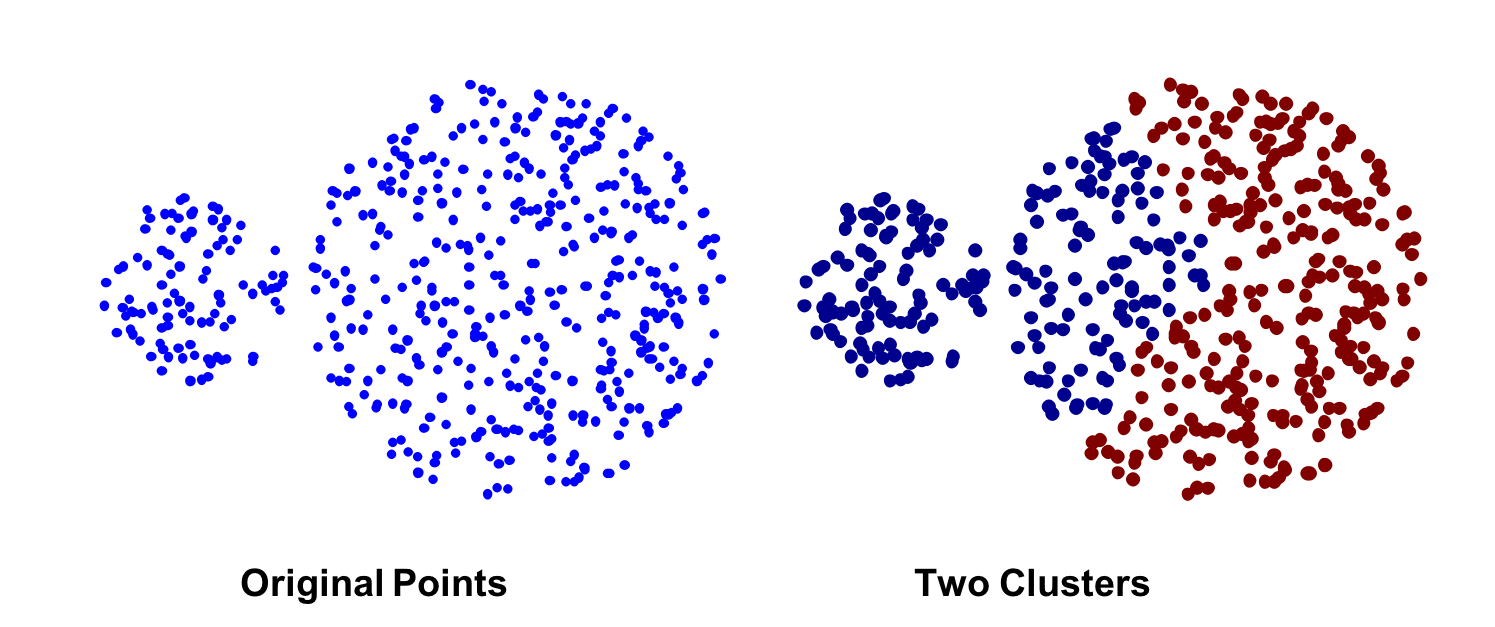
Group Average: is a compromis between single and complete Link.

Ward’s Method: Similarity of two clusters is based on the increase in squared error when two clusters are merged.

DBSCAN

lDBSCAN is a density-based algorithm.

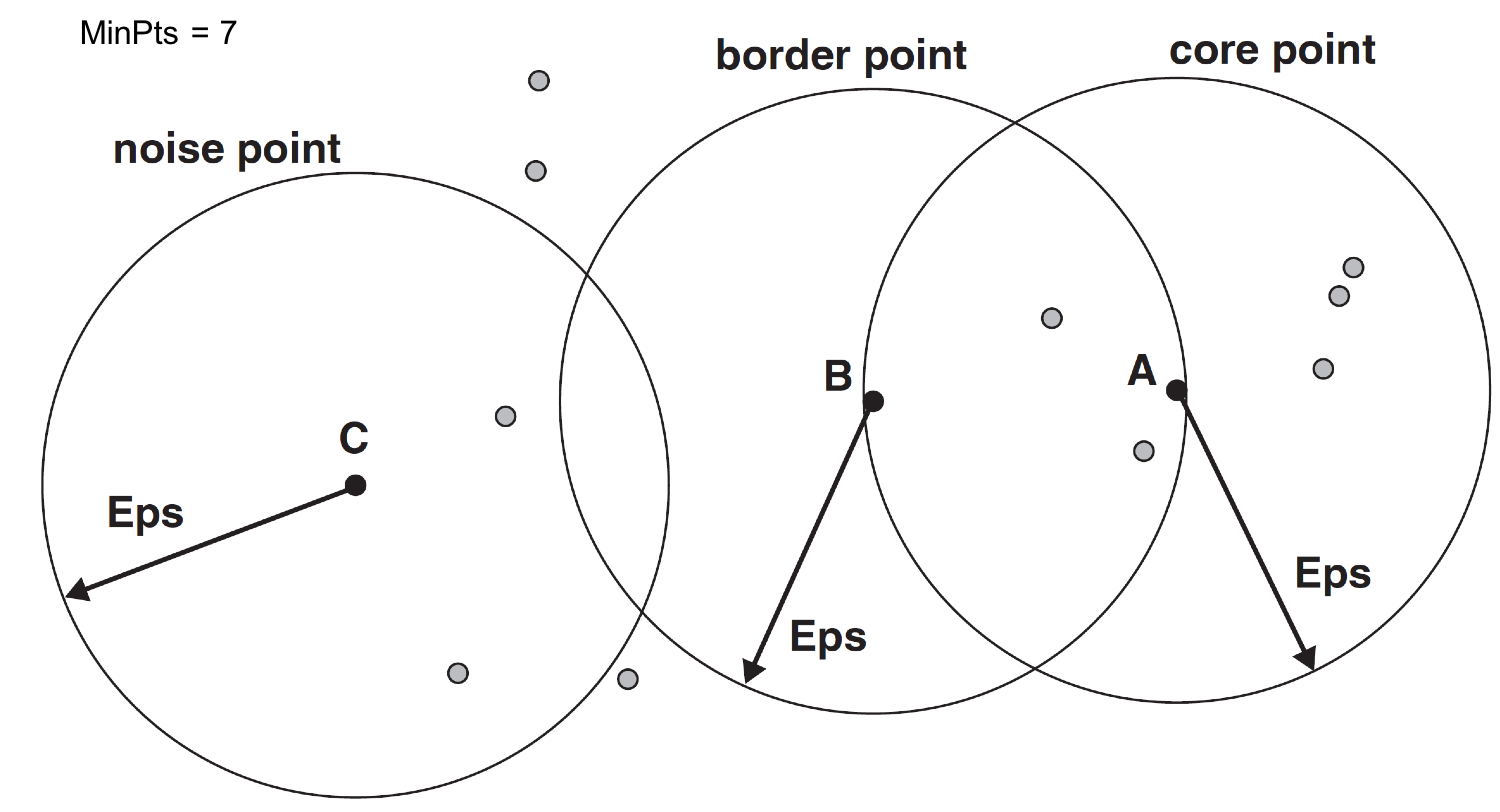
• Density = number of points within a specified radius (Eps)
• A point is a core point if it has at least a specified number of points (MinPts) within Eps
• A border point is not a core point, but is in the neighborhood of a core point
• A noise point is any point that is not a core point or a border point

The DBSCAN algorithm is resisitant to noise, and can handle clusters of different shapes and sizes.

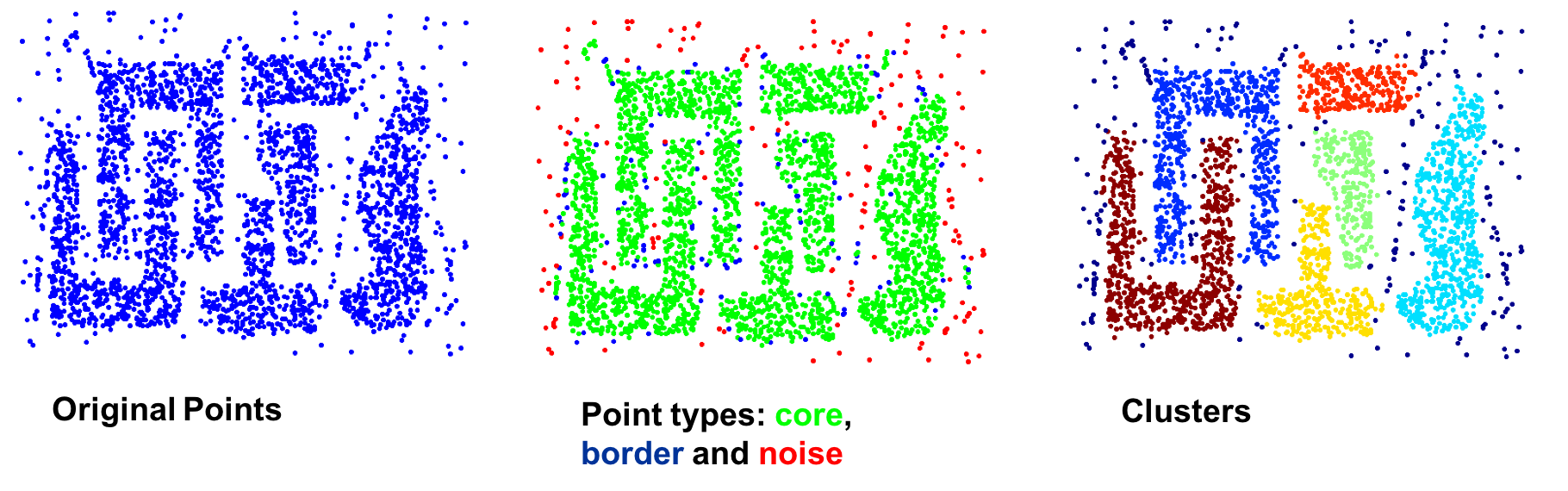
DBSCAN can fail when the data has varying densities and high-dimensional data.

Cluster Validity

Entropy and SSE can be used to evaluate the performance of clustering.